Afrânio Rubens de Mesquita
(IOUSP)& Keith Dyer (Liverpool University, UK)
Resumo
Foi
desenvolvido um procedimento, à partir das Equações
de Laplace de Marés, que permite expressar a forma quadrática
de dissipação de energia, em termos do coeficiente de fricção
K em freqüências harmônicas. Por meio da transformada
de Fourier são obtidas as diferenças de fase das componentes
de correntes e de suas correspondentes amplitudes de nível do mar,
que são utilizadas na estimativa de K. Estimativas com esse procedimento
e medições de correntes médias no Canal Western Solent,
UK e medições em ponto fixo no Canal de Maré em Cananeia,
Brasil produziram valores de K entre 2 a 5 x 10![]() ,
condizentes com determinações obtidas por outros meios, validando
o procedimento e abrindo uma nova possibilidade de estudo das componentes
não lineares, geradas pelas forçantes do Potencial Gerador
de Marés.
,
condizentes com determinações obtidas por outros meios, validando
o procedimento e abrindo uma nova possibilidade de estudo das componentes
não lineares, geradas pelas forçantes do Potencial Gerador
de Marés.
Abstract
From
the Tidal Equations of Laplace, a method was developed expressing the quadratic
form of the dissipation term, as a harmonic frequency dependent coefficient
K . By means of the Fourier Transform, phase of currents and the tidal
heights allowed the estimation of the phase angle differences, which were
used to estimate the K values . Based on these procedures and from measurements
of the Channel mean current of the Western Solent, UK and measurements
at a fixed point in the Cananeia Canal, Brazil, values of K within 2 to
5 x 10![]() were calculated, well within previous determinations by other methods,
validating the procedure and opening a new possibility of studying non
linear components generated from the Tide Potential Generating Forces.
were calculated, well within previous determinations by other methods,
validating the procedure and opening a new possibility of studying non
linear components generated from the Tide Potential Generating Forces.
Histórico
O
mecanismo de dissipação de energia das marés nos oceanos
, de longa data estabelecido por Taylor (1919) , no estudo de correntes
em áreas de plataforma, foi escrito em termos da força de
fricção na forma : F = K u ![]() , sendo K o coeficiente de fricção e u o valor
da velocidade do fluxo de correntes próximo ao fundo oceânico.
Os valores adimensionais estimados de K foram da ordem de 0,002.
, sendo K o coeficiente de fricção e u o valor
da velocidade do fluxo de correntes próximo ao fundo oceânico.
Os valores adimensionais estimados de K foram da ordem de 0,002.
Desde então, métodos de avaliação da energia dissipada nos oceanos foram desenvolvidos e utilizados em escala global, sem que houvesse necessidade de explicitar a natureza do mecanismo físico com que as correntes oceânicas efetivamente eram dissipadas, Spencer Jones (1930).
Uma conseqüência geofísica estreitamente correlacionada à dissipação de energia das marés nos oceanos, utilizada por esses estudos, é a aceleração secular do movimento de rotação da Terra . A troca de momento angular entre Terra e Lua, em razão da dissipação é de tal ordem, que hoje em dia a velocidade de rotação da Terra é menor do que a observada, por exemplo, há 3000 anos atrás e muito menor ainda do que quando da definição do satélite Lua, há bilhões de anos atrás. Da mesma forma que a Terra perde velocidade de rotação, a Lua em sua órbita se distancia da Terra de forma a manter, por conservação do momento angular, o momento angular do sistema Terra - Lua. Lambeck (1975).
Outros métodos,entretanto, levam em consideração a energia dissipada pela turbulência associada ao fluxo de marés, fenômeno descrito no século XIX, Reynolds (1883), que aquece o planeta e a irradia para o espaço . O fluxo turbulento é complexo e de difícil introdução nas equações de Laplace, mas vários estudos baseados nas teorias de Prandlt (1925), Von Karman (1948) sobre o fluxo turbulento, mostraram que eles são importantes e passíveis de incorporação nas equações, na explicitação dos processos físicos de dissipação global de energia.
Por essas razões, esses procedimentos tem sido renovados e considerados importantes nos desenvolvimentos que possibilitam estimar o coeficiente de fricção K nas equações de Laplace e desse esforço vários resultados significativos têm sido obtidos.
Os primeiros estudos dos processos turbulentos nos oceanos datam do início do século XX e eram muito difíceis de serem feitos, principalmente pelo fato de que não haviam equipamentos que permitissem a medição de correntes com a necessária precisão para os seus desenvolvimentos .
Em 1936 Doodson construiu um correntômetro elétrico capaz de medir flutuações com períodos de 1 segundo, iniciando um processo que, juntamente com novas técnicas amostrais de medição de correntes à bordo de embarcações, conduziu a contribuições relevantes na determinação de K, ( Bowden,1962).
Paralelamente a esses desenvolvimentos, outros estudos (Franco, 1975), baseados na teoria do Potencial Gerador de Marés e na solução das equações de Laplace, por Saint Venan, abriram a possibilidade de se entender como podem ser descritas, em termos dos movimentos da Lua e do Sol, as componentes não lineares de Marés, derivadas do movimento turbulento das correntes de marés.
O mecanismo de geração das componentes de pequeno fundo (Marone , 1991), foi estudado através de métodos espectrais mais acurados, como o biespectro, que se destinaram a examinar processos físicos derivados de interações não lineares e permitiram examinar a produção de múltiplas interações das componentes astronômicas, antes não explicitadas com os métodos usuais. Ainda dentro desse estudo foi estabelecido um critério estatístico pelo qual qualquer componente de Fourier pode ser determinada através de medições de nível do mar com desvio padrão conhecido.
O termo advectivo, juntamente com o termo de fricção, foram identificados, nas equações do movimento de Laplace, como geradores de componentes não lineares pares e impares, respectivamente, (Godin, 1968), na composição do conjunto de componentes de pequeno fundo em todas as áreas dos oceanos. Em particular, na região da plataforma Sudeste do Brasil, as análises das medições de correntes obtidas em várias profundidades, Mesquita e Harari, (2000), confirmaram a ocorrência de componentes astronômicas de correntes de marés impares e pares (diurnas, semidiurnas e terdiurnas) de magnitude apreciável ( de 3 a 11cm/s) com indicação clara de ocorrência de componentes não lineares na área .
A profusão de componentes astronômicas impares e pares, então identificadas, levou ao desenvolvimento de métodos espectrais , baseados na variação das fases das componentes harmônicas, que permitiram identificar a ocorrência e escolher as componentes não lineares de marés com grande certeza estatística França (1988). As componentes M4 , MK4 e MN4 foram as únicas na plataforma continental Sudeste do país a passar pelo teste, enquanto que um método desenvolvido, de perturbações na solução das equações permitiu novos avanços no exame dos processos dissipativos das marés.
Por outro lado, os recentes desenvolvimentos de equipamentos de medições de correntes, por métodos acústicos, permitiram o exame das correntes de marés nas três direções Cartesianas com alta precisão e grande adensamento amostral, que possibilitaram identificar a ocorrência de estruturas coerentes no fluxo de marés no Mar de Cananeia e na região costeira próxima (Corrêa, 2001). Esta verificação introduz novo elemento de natureza não estatística na definição da tensão de cisalhamento em fluxo de marés, permitindo uma melhor descrição do coeficiente K, cuja forma e composição em termos das componentes astronômicas é o desafio a alcançar.
Medições de Correntes
As medições de correntes a que se refere o presente estudo sobre o coeficiente K foram feitas no canal Western Solent (Mesquita 1972), que separa a Ilha de Wight da Ilha principal Britânica. A Figura 1 mostra o Canal da Mancha com os indicativos das linhas de mesma fase e de mesma amplitude da onda de Maré estacionária, que lá ocorre, que tem ponto anfidrômico degenerado nas proximidades de Stonehenge.

Fig 1; Canal da Mancha e o Canal Western Solent indicado por Yarmouth
e Calshot
O Canal de Western Solent é mostrado na Fig 2 , onde Calshot e Yarmouth indicam os locais onde foram obtidas informações simultâneas de alturas de nível do mar.Os pontos P1, P2, P3 indicam os locais onde os três barcos usados para as medições ficavam ancorados, de modo a permitir que medições fossem feitas nos dias 27/05/71 e 02/06/71, nas profundidades de 1m , 2m e 4m acima do fundo e 2 m abaixo da superfície, em um canal cuja profundidade média é de 15 metros e largura média de 2,5 Km, durante um período de 12 horas.
Foram calculadas as correntes médias na vertical e na secção transversal e o fluxo considerado unidimensional. No dia 3/08/71 foram feitas medições ao longo da seção longitudinal do canal, com as embarcações ocupando as posições P2, P4 e P5. que serão utilizadas na continuidade do presente estudo.
A Análise Realizada
A análise supôs a passagem da onda livre de maré no canal , que a tensão de cisalhamento variou linearmente com a profundidade, que a lei logarítmica de distribuição de velocidade das correntes é verificada até a superfície, que a influência da aceleração de Coriolis é
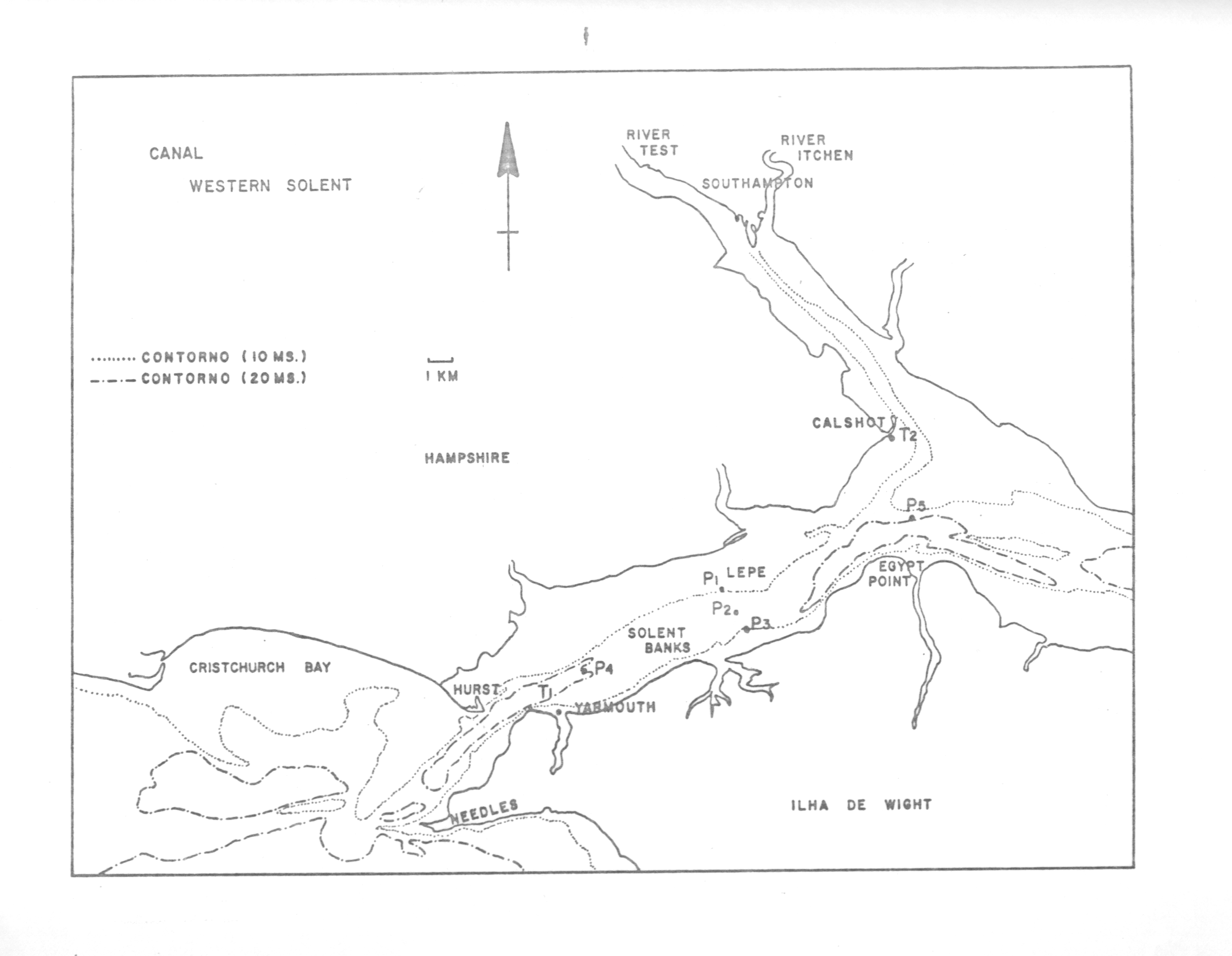
Fig 2 - Canal Western Solent (WS), no Estuário de Southampton indicado por suas extremidades : Yarmouth e Calshot. Os pontos P1,P2,P3,P4 e P5 indicam os locais ocupados por embarcações, onde foram obtidos os valores de correntes .
desprezível,
que o termo advectivo é desprezível, que a tensão
na superfície produzida pelos ventos é pequena e que, por
conseguinte, o fluxo é acelerado pelo gradiente de pressão,
-![]() ,
sendo dissipado em cada ciclo através da forma quadrática
,
sendo dissipado em cada ciclo através da forma quadrática![]() do
termo de dissipação.
do
termo de dissipação.
As Equações
de Laplace nessas condições assumem a forma :
![]() ( 1 )
( 1 )
![]() ,
,
onde ![]() corresponde à média no tempo, em intervalos de 5 minutos.
corresponde à média no tempo, em intervalos de 5 minutos.
Utilizando
o termo quadrático de Rx = Ku![]() /H
e integrando-se na vertical obtêm-se,
/H
e integrando-se na vertical obtêm-se,
após
algum cuidado, onde ![]() ,
agora, corresponde à média nas direções vertical
e transversal do canal:
,
agora, corresponde à média nas direções vertical
e transversal do canal:
:
![]() (
2 )
(
2 )
Admitindo-se
que:
![]() ,
(2 a)
,
(2 a)
onde ![]() é a altura da maré e
é a altura da maré e ![]() a profundidade média do Canal e que a variação da
corrente média e a variação da maré possam
ser escritas com diferença de fase (
a profundidade média do Canal e que a variação da
corrente média e a variação da maré possam
ser escritas com diferença de fase ( ![]() ) na forma:
) na forma:
![]()
e a variação da corrente seja descrita por : ( 3 )
:
![]() ,
,
obtêm-se,
substituindo-se esses valores nas equações de Laplace, após
algum labor, ver Apêndice :
![]() ,
( 4 )
,
( 4 )
que
é a solução procurada, sujeita a certas condições
em um canal.
Para
cada freqüência ( ![]() ) a relação (4) acima permite determinar o valor de K,
uma vez conhecido o valor da defasagem (
) a relação (4) acima permite determinar o valor de K,
uma vez conhecido o valor da defasagem (![]() )
entre a corrente e altura de maré no local de medida e o valor da
amplitude de corrente u(x), juntamente com o valor da profundidade média
)
entre a corrente e altura de maré no local de medida e o valor da
amplitude de corrente u(x), juntamente com o valor da profundidade média ![]() do Canal.
do Canal.
Os
valores de (![]() )
podem ser obtidos através da análise de Fourier dos dados
simultâneos de correntes e alturas da maré no mesmo local
das medições de correntes, conforme mostra a Fig 3. Na parte
superior, são mostradas as alturas de marés obtidas em Yarmouth
e Calshot e a curva intermediária, desenhada mais abaixo, correspondente
aos valores da altura de marés no meio do Canal, durante o dia de
medições de 06/07/71.
)
podem ser obtidos através da análise de Fourier dos dados
simultâneos de correntes e alturas da maré no mesmo local
das medições de correntes, conforme mostra a Fig 3. Na parte
superior, são mostradas as alturas de marés obtidas em Yarmouth
e Calshot e a curva intermediária, desenhada mais abaixo, correspondente
aos valores da altura de marés no meio do Canal, durante o dia de
medições de 06/07/71.
A onda semidiurna de quadratura da Fig 3 é dividida nas partes Inercial, em que o fluxo médio de correntes é aproximadamente nulo, Acelerada , onde os gradientes de pressão são fortes, e Estacionária, onde a corrente média é aproximadamente constante e o termo Dissipativo ,em valor absoluto, é aproximadamente igual ao termo de Gradiente de Pressão .
Da parte Estacionária obteve-se, com a equação de trabalho (2), um valor de K = 0,0055 para maré de quadratura . Valores para a maré de Sizygia (24/5/71) forneceram valores K = 0,0035.
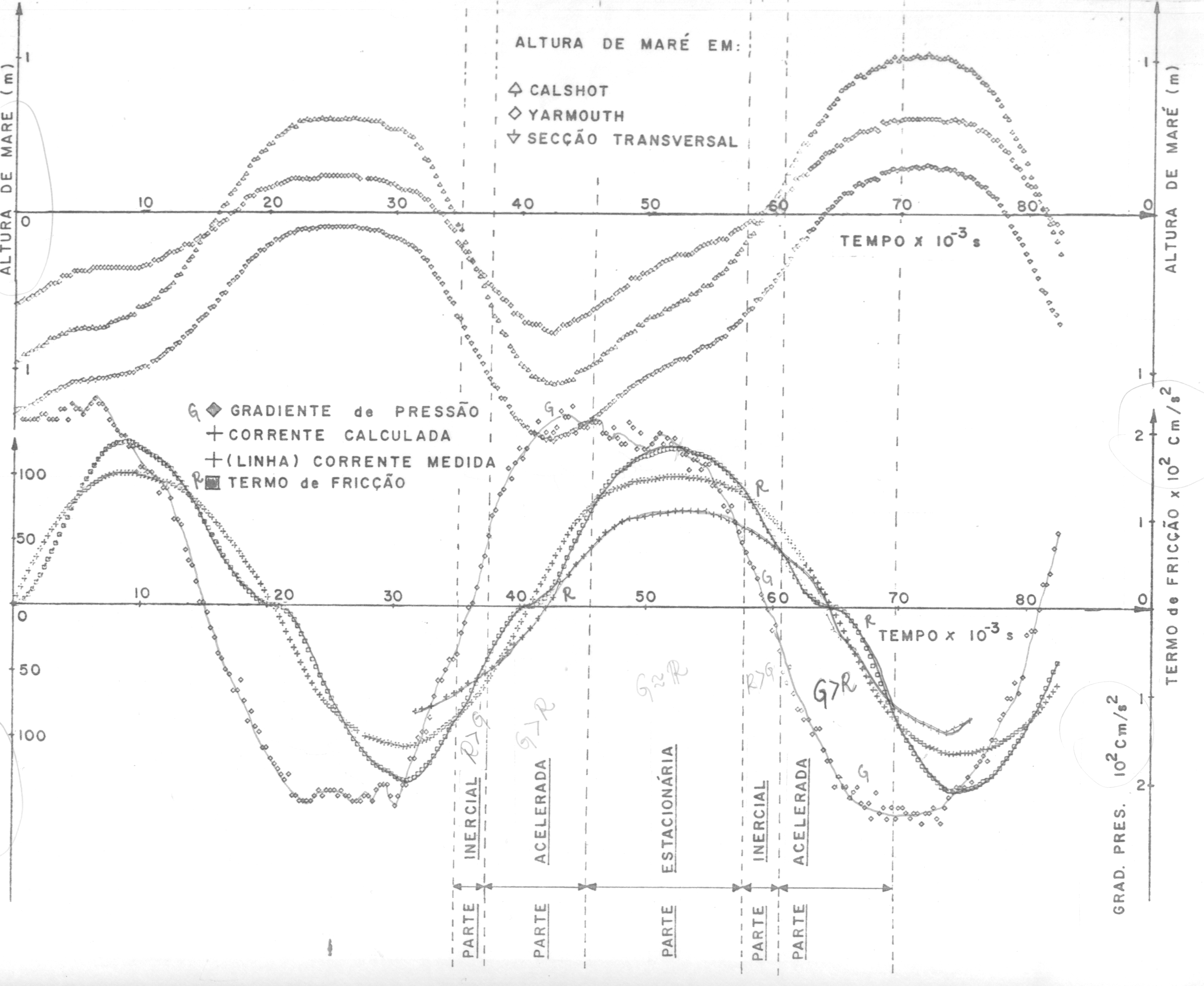
Fig 3- A onda de marés e suas subdivisões Inercial,Acelerada e Estacionária no WS.
Na parte de baixo da Figura 3 são mostrados os valores dos gradientes de pressão, do termo de dissipação, a corrente prevista por método Runge Kutta de quarta ordem, juntamente com os valores efetivamente medidos da corrente média (curva contínua) no meio do Canal. Se os dados de correntes forem de mesmo comprimento dos dados de altura de marés e longos (1 ano, por exemplo) poderão ser usadas as constantes harmônicas de pequeno fundo, definidas por Franco (1975) para a determinação dos valores de K .
Os
valores de K obtidos, com apenas 6 horas de medições
, através da comparação da integração
da equação (2) com as medições da corrente
média no Canal Western Solent (WS), realizadas no ano de 1971, em
medições horárias, indicaram para a componente quarto
diurna, valores da ordem de 2,6 x 10![]() ,
que se comparam bem com os valores obtidos por Taylor em 1919 e com os
obtidos nas partes estacionárias e aceleradas da onda, como acima
indicado, garantindo a validade dos procedimentos adotados nesta análise.
,
que se comparam bem com os valores obtidos por Taylor em 1919 e com os
obtidos nas partes estacionárias e aceleradas da onda, como acima
indicado, garantindo a validade dos procedimentos adotados nesta análise.
Para as componentes semidiurnas e sextodiurnas, entretanto, os valores foram imprecisos, o que se deve, provavelmente, à pequena quantidade de dados de correntes médias do Canal utilizadas no cálculo. Tais componentes poderão ser melhor estimadas através de um conjunto mais longo de medições da corrente média, um mês por exemplo.
Discussão e Conclusão
Os resultados presentes, obtidos para os valores de K, abrem a possibilidade para o exame do termo quadrático de dissipação de energia das marés, através da Análise de Fourier . A expressão a que se chegou para K não faz distinção entre termos pares e ímpares conforme (Godin 1968) e pode, em principio, ser utilizada para todas as componentes de pequeno fundo, com origem nas componentes astronômicas para a estimava, quer sejam originárias do componente advectivo, ou do termo de fricçãodas equações de Laplace. Também não pode distinguir as componentes não lineares identificadas por Marone (1991) na análise de biespectros de marés, bem como as componentes não lineares identificadas por França (2000) na plataforma sudeste .
Essa indistinção foi utilizada na composição do espectro dos valores de K calculados com dados de corrente do Canal de Maré de Cananeia, obtidos por Miranda (comunicação pessoal), no período de 28/10 a 27/11 de 1996 . Também não há como considerar, na análise desses dados, a eliminação da contribuição das estruturas coerentes identificadas por Corrêa (2002 ) no mar de Cananeia, desde que o termo dissipativo da equação do movimento, escrito na forma quadrática, supostamente, deve incorporar todas as formas de contribuições não lineares, inclusive as derivadas das estruturas coerentes.
As determinações de K mostradas no espectro da Fig 4, não obstante, permitem identificar valores diferentes para cada freqüência do espectro de Fourier. Valores de K indicados com círculos cruzados correspondem a cálculos feitos, no Canal de Cananeia, com valores de profundidade média H =700cm ; valores indicados com cruzes (x ) indicam profundidade média H =600cm e valores indicados com (+) indicam valores obtidos com profundidade média igual a 500cm, que mostram a sensibilidade da formulação alcançada na estimativa do coeficiente de fricção.
Como
pode ser visto, a maioria dos valores de K está compreendida
entre -0.01 e 0.01 e se distribui ao longo de faixas de freqüências
de Fourier correspondentes às faixas de longo termo, diurnas, semidiurnas
e terdiurnas, das componentes harmônicas de maré. Estima-se
que as faixas não correspondentes às marés, produzam
valores maiores do que os mostrados na Fig 4.Valores negativos ou positivos
de K podem ser determinados, dependendo como se compõem as
fases (![]() )
das componentes de marés e de suas correspondentes correntes .
)
das componentes de marés e de suas correspondentes correntes .
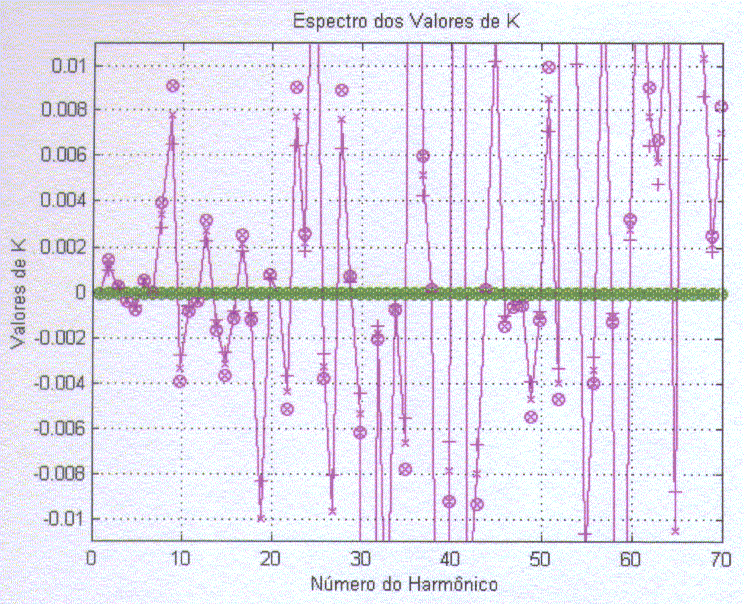
Figura 4 – Valores do Coeficiente de Fricção K calculados no Canal de Cananeia.
A
expressão ( 4) que define K nos presentes estudos,
indica que o mesmo valor deverá ser obtido em todas as freqüências
e que também deve haver uma dependência inversa de K
com as amplitudes das componentes das correntes, isto é , componentes
de maior freqüência têm amplitudes, em geral, menores
e, por conseguinte, produzem maiores valores de K. Para que isso
não ocorra deve-se esperar que os valores de (![]() )
das diferenças de fase entre correntes e níveis de maré
devam ser progressivamente menores para maiores freqüências,
de forma a permitir que as estimativas de K tenham o mesmo valor.
)
das diferenças de fase entre correntes e níveis de maré
devam ser progressivamente menores para maiores freqüências,
de forma a permitir que as estimativas de K tenham o mesmo valor.
O
número de harmônicos na Fig 4 foi calculado sobre uma série
de 480 horas, ou 20 dias de dados horários de marés, simultâneos
às medições de correntes, feitas à 2m acima
do fundo. Dessa forma, ao harmônico de número 40 corresponde
a freqüência 40/480 = 4/48 = 1/12 ciclos por hora, que corresponde
ao período de 12 horas, período semidiurno das marés
. Nessa faixa, os valores absolutos se distribuem, na Figura 4, em torno
de K = 4,3 10![]() .Na faixa de 24 horas, períodos diurnos das marés em torno
de K=0.005, enquanto na faixa das marés terdiurnas os valores
absolutos se distribuem em torno de K= 0.002.
.Na faixa de 24 horas, períodos diurnos das marés em torno
de K=0.005, enquanto na faixa das marés terdiurnas os valores
absolutos se distribuem em torno de K= 0.002.
Muito embora esses valores estejam próximos aos obtidos através de outros métodos, Mesquita (1972,1981), existem variações dos valores de K, nas diferentes faixas de freqüências, que apenas poderão ser estimadas à partir de um conjunto maior de dados de correntes em um canal, quando a corrente média vertical e transversal puder ser medida para a o estudo da composição das freqüências definidas no potencial gerador de marés.
Deve
se notar que os valores de correntes foram obtidos em profundidade de 2m,
que correspondem em média a 1/2 da corrente da superfície.
(Miranda, comunicação pessoal) . Um valor dessa grandeza
deve, segundo a expressão ( 4 ), diminuir os valores obtidos para
K
na mesma proporção e os valores de(![]() )
deverão se modificar de forma consistente a se poder estimar esses
valores.
)
deverão se modificar de forma consistente a se poder estimar esses
valores.
Estudos que venham a estimar os valores de K, através das componentes de Fourier, poderão contribuir para o melhor entendimento dos processos dissipativos das equações de Laplace (1) , bem como na composição das componentes de pequeno fundo das marés, proposta por Franco (1985).
Agradecimentos
Á Fundação Ford e Conselho Britânico pela bolsa de estudo concedida ao primeiro autor, durante o período em que esteve na Universidade de Southampton, Inglaterra. Ao Departamento de Oceanografia da Universidade de Southampton e à Administração do Porto de Southampton, que possibilitaram a obtenção dos dados de medições utilizados deste trabalho.
Referências
Bowden, K.F. (1962). Measurements of turbulence near the sea Bed in a Tidal Current.J. Geophys. Res.67:3181- 3186.
Corrêa, M. A. (2001). Contribuição ao Estudo dos Processos Turbulentos Oceânicos na Camada Limite de Canal de Maré. Tese de Doutorado . Inst. oceanogr. Univ. S. Paulo. SP. 300p.
Doodson, A. T. (1936). Ocean Tides. Advances in Geophys, 5 :117-152.
França, C. A. de S. (1988). Estudo da Geração das Componentes de Maré de Pequeno Fundo na Costa Sudeste Brasileira. Dissertação de Mestrado . Inst. Oceanogr. Univ. S Paulo. SP. 254p.
Franco, A. dos S. (1975). Componentes Harmônicas da Maré em Pequenos Fundos. Tese de Doutorado . Escola Politécnica da Universidade de S Paulo. SP. 64p.
Godin, G. (1972). Analysis of Tides .Livepool University Press. 250 p
Lambeck, K. (1975). Effects of Tidal Dissipation in the Oceans on the Moon´s Orbit and the Earth´s Rotation. J. geophys.Res.,80:2917-2925.
Marone, E. (1991). Processamento e Análise de Dados de Mar´: discurso dos Métodos. Uma Aplicação aos Registros Maregráficos e Meteorológicos do Litoral Sul – Leste de Buenos Aires, Argentina (38 03 S a 39 23 S) . Tese de Doutorado .Inst. oceanogr. Univ. S Paulo.SP. 231p.
Mesquita, A. R. de (1972). Studies on the Mean Flow of the Western Solent Tidal Channel. Mphil Thesis . Univ.Southampton. 170p.
Mesquita A. R. de (1981). Dissipação de energia em Canal de Maré. Tese de Doutorado. Inst. oceanogr. Univ. S. Paulo.SP.,249p.
Mesquita, A. R. De; Harari, J. (2000). On the Sea Level Network and Circulation in the South Eastern Brazilian Shelf .. In Ocean Circulation Science Derived from the Atlantic, Indian and Arctic Sea Level Networks .- Editor - Gary Mitchum - UNESCO WSR No 171 - Annex III : 34-51.
Prandlt, L.(1925).Über die ausgebildete Turbulenz.. ZAMM 5,136-139 and Proc.2nd Intern. Congr. Appl. Mech., Zurich 1926,62-75.
Taylor, G. I . (1919). On tidal friction in the Irish Sea. Phil. Trans. R. Soc. London A, 220:1-33.
Von
Karman, Th (1930). Mecahnische Ahnliechkeit und Turbulenz.Nach. Ges.Wiss.Göttingen.Math.Phys.Klasse,
58
Apêndice
Nas
equações de Laplace indicadas pelas expressões ( 1
) que definem o fluxo unidimensional aplicado à corrente média ![]() ,
seja :
,
seja :
![]() e
que
e
que ![]() <<
<<![]() tal que:
tal que: ![]() (5)
(5)
Sejam
também ![]() e
e ![]() , (6)
, (6)
as
soluções das equações de Laplace (1), onde
(![]() )
é uma freqüência e o ângulo (
)
é uma freqüência e o ângulo (![]() )
a diferença de fase entre
)
a diferença de fase entre ![]() e
e ![]() .
.
Derivando-se a primeira equação de Laplace (1), em relação a ( x ) e subtraindo-se da derivada da segunda equação (1), em relação a ( t ) obtêm-se:
![]() =0
, (7)
=0
, (7)
mas
da segunda equação de Laplace (1), obtêm-se:
![]() ,
que substituída na equação (7) acima produz:
,
que substituída na equação (7) acima produz:
![]() ,
(8)
,
(8)
que
é uma expressão somente na variável (![]() )
a ser estimada através das equações de perturbação
do sistema (6) .
)
a ser estimada através das equações de perturbação
do sistema (6) .
De
fato, derivando-se a primeira das equações (6) duas vezes
em relação ao tempo ( t ) obtêm-se:
![]() e
e ![]() . (9)
. (9)
Derivando-se novamente a expressão primeira das equações (6), duas vezes, mas agora em relação a variável (x):
![]() e
e ![]() . (10)
. (10)
Substituindo-se a primeira e a segunda das equações (9) e a segunda das equações (10) na equação (8), obtêm-se:
![]() (11)
(11)
que é uma equação diferencial a derivadas totais, cuja solução geral é dada por:
h(x)=![]() , onde
, onde ![]() e
e ![]() , sendo
, sendo ![]() ,
,
![]() e
e ![]()
![]() constantes a ser determinadas. Dessa forma pode-se escrever a solução
da equação (8) como:
constantes a ser determinadas. Dessa forma pode-se escrever a solução
da equação (8) como:
![]() (12)
(12)
Substituindo-se
a equação (12) e a segunda equação (6) na primeira
equação de Laplace (1), obtêm-se:
![]() ,
(13)
,
(13)
cujas
constantes ![]() ,
, ![]() e
e ![]() podem ser determinadas através das condições de contorno
como:
podem ser determinadas através das condições de contorno
como:
![]() para
para ![]() ,
na boca do canal de maré. Nessas condições a equação
(13) se reduz a:
,
na boca do canal de maré. Nessas condições a equação
(13) se reduz a:
 .
(14)
.
(14)
Definindo-se
C=![]() , pode-se escrever
, pode-se escrever
![]() .
(15)
.
(15)
Igualando-se
as partes reais e imaginárias de (15) obtêm-se:
![]() e
e ![]() .
(16)
.
(16)
Dividindo-se as expressões (16):
![]() .
(17)
.
(17)
Desenvolvendo-se
(17) para a separação de ![]() chega-se a:
chega-se a:
![]() (18)
(18)
Usando-se
de (15) , ![]() e desenvolvendo-se para separar
e desenvolvendo-se para separar ![]() ,
obtêm-se:
,
obtêm-se:
![]() ,
onde s=
,
onde s=![]() . (19)
. (19)
Usando-se
(18) e desenvolvendo-se para separar as funções seno(![]() )
e coseno(
)
e coseno(![]() ),
obtêm-se:
),
obtêm-se:
![]() (20)
(20)
Substituindo-se (19) em (20) obtêm-se:
![]() .
(21)
.
(21)
Substituindo-se
(21) em (2 a), ou (5), obtêm-se a expressão procurada para
o coeficiente de fricção:
![]() ,
(22)
,
(22)
onde ![]() , conforme expresso na equação (5) e
, conforme expresso na equação (5) e ![]() a corrente média da onda de freqüência
a corrente média da onda de freqüência ![]() , conforme expressão (6).
, conforme expressão (6).
Substituindo-se
os valores de ![]() e
e ![]() em (22) obtêm-se:
em (22) obtêm-se:
 (23)
(23)
Efetuando-se as operações indicadas obtêm-se:
![]() ,
(24)
,
(24)
ou ![]() . (25)
. (25)
Então,
para locais onde ![]() pode-se escrever:
pode-se escrever:
![]() .
(26)
.
(26)
Que
é igual a expressão (4). Para o Western Solent, onde a profundidade
média do Canal é ![]() e as amplitudes das ondas de freqüências
e as amplitudes das ondas de freqüências ![]() que compõem a maré são menores do que
que compõem a maré são menores do que ![]() a expressão pode ser usada para se estimar os valores do coeficiente
de fricção. Para o Canal de Cananeia onde a profundidade
é
a expressão pode ser usada para se estimar os valores do coeficiente
de fricção. Para o Canal de Cananeia onde a profundidade
é ![]() e a maior amplitude da componente de freqüência
e a maior amplitude da componente de freqüência ![]() é menor do que
é menor do que ![]() e a razão profundidade / amplitude é maior do que 4 , a expressão
(26) também pode ser usada para o cálculo de K. cqd.
e a razão profundidade / amplitude é maior do que 4 , a expressão
(26) também pode ser usada para o cálculo de K. cqd.