MODELING THE TIDAL CIRCULATION IN CANANEIA - IGUAPE ESTUARY
AND ADJACENT COASTAL AREA (SAO PAULO, BRAZIL)
Simone Seixas Picarelli 1 & Joseph Harari 1 & Ricardo de Camargo 2
simpic@usp.br & joharari@usp.br & ricamarg@model.iag.usp.br
1 Institute of Oceanography of Sao Paulo University
2 Institute of Astronomy, Geophysics and Atmospheric Sciences of Sao Paulo University
Sao Paulo, SP – Brazil
The tidal
circulation in Cananeia – Iguape estuary is simulated using a version of
the Princeton Ocean Model – POM (Blumberg & Mellor, 1987), a three-dimensional
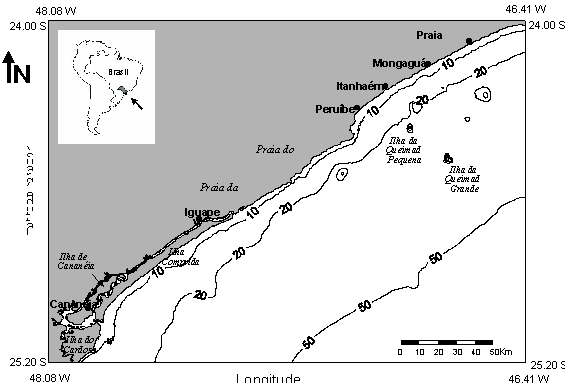
sigma coordinate model. Figure 1 shows the region of the basic regular grid
considered in the study, with horizontal spacing of 1 Km, which has embedded
the estuary of interest and extends until the isobath of 50 m. High resolution
grids (with 100 m spacing) were nested in the basic one, in order to obtain
details of the circulation in internal shallow areas.

The basic grid used boundary conditions specified by Harari & Camargo (1994) shelf model, by composing the oscillations of tidal components Q1, O1, P1, K1, N2, M2, S2, K2 and M3, which correspond to more than 90% of the tidal energy in this shelf. Both basic and nested grids adopted 11 sigma levels, uniform temperature and salinity fields and started from rest. They run 29 days and the resulting time series of elevations and currents were analyzed through the Harmonic Method of Tidal Analysis (Franco & Harari, 1987; Franco, 1988).
Instantaneous results obtained in the nested grids of the estuary are shown on Figure 2, relative to maximum ebbing currents during spring tides; a significant increase of these currents is observed at the Northern and Southern mouths of the estuary, reaching nearly 1 m/s.
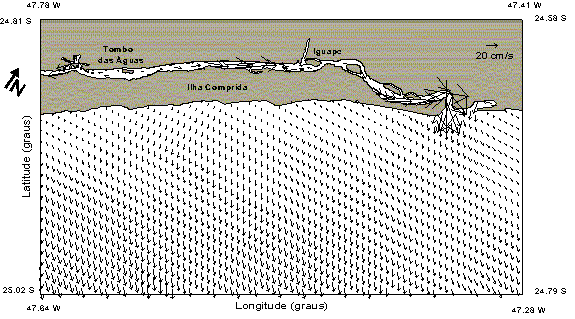
Fig. 2a: Ebbing currents during spring tides in the Northern part of the estuary
(22:00 GMT 07/February/1997)
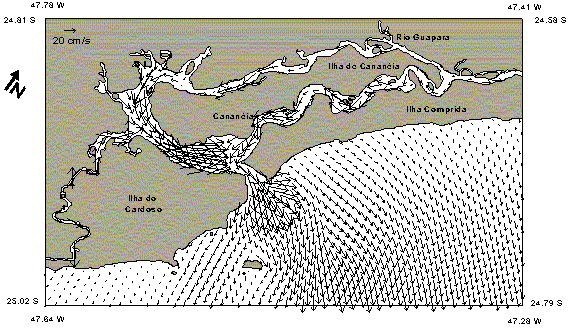
Fig. 2b: Ebbing currents during spring tides in the Southern part of the estuary
(22:00 GMT 07/February/1997)
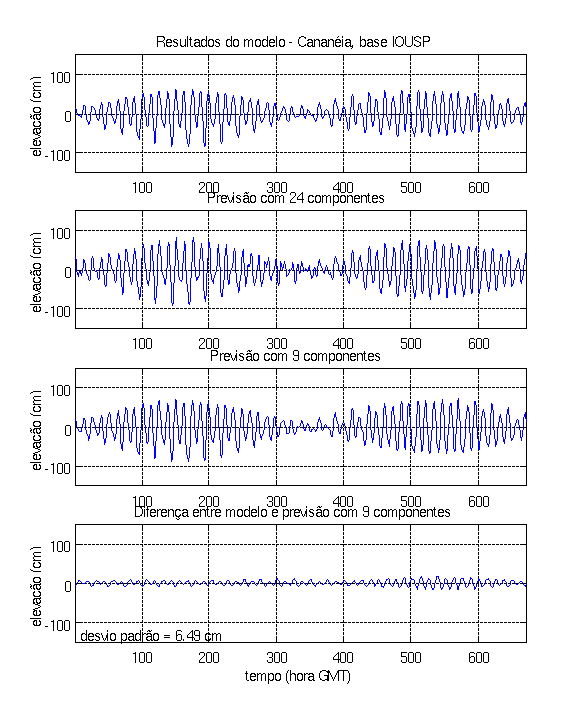
The model results were compared to observations in the tidal station of Cananeia (25° 01’ S 047° 55.5’ W), shown on Figure 3, which contains the time series of elevations generated by the model, a harmonic prediction with 24 tidal components, another harmonic prediction (with the same 9 components used in the model) and the difference between the model output and the last harmonic prediction: this difference has a standard deviation of 6.49 cm.
The harmonic analysis of the time series generated by the model output produced cotidal maps, as presented on Figure 4 for M2 component (relative to the basic grid). In fact, the number of results given by a three-dimensional model is quite large – cotidal maps, current ellipses (at levels of interest), depth-mean currents, volume and mass transports, vertical profiles of currents, etc …
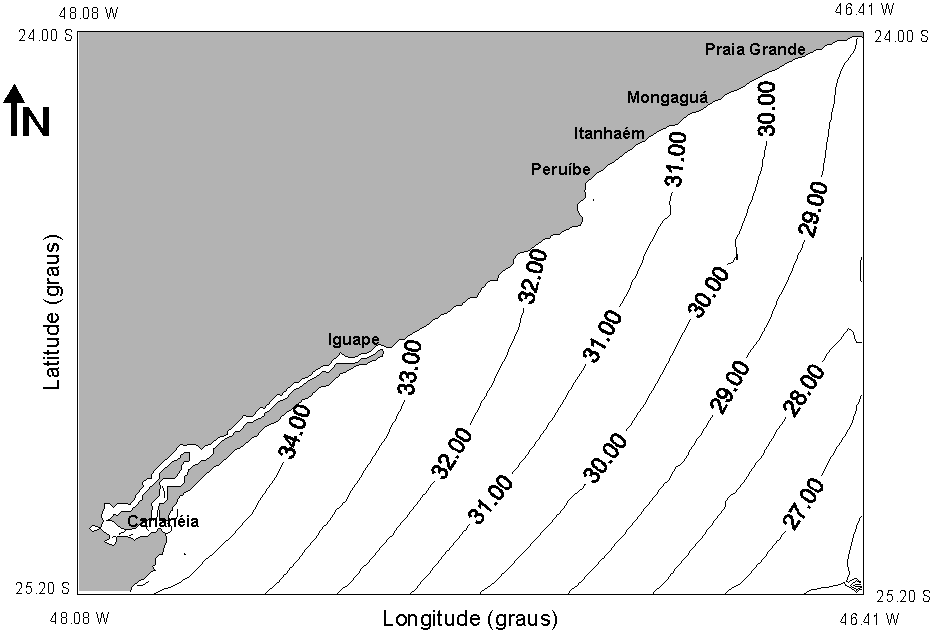
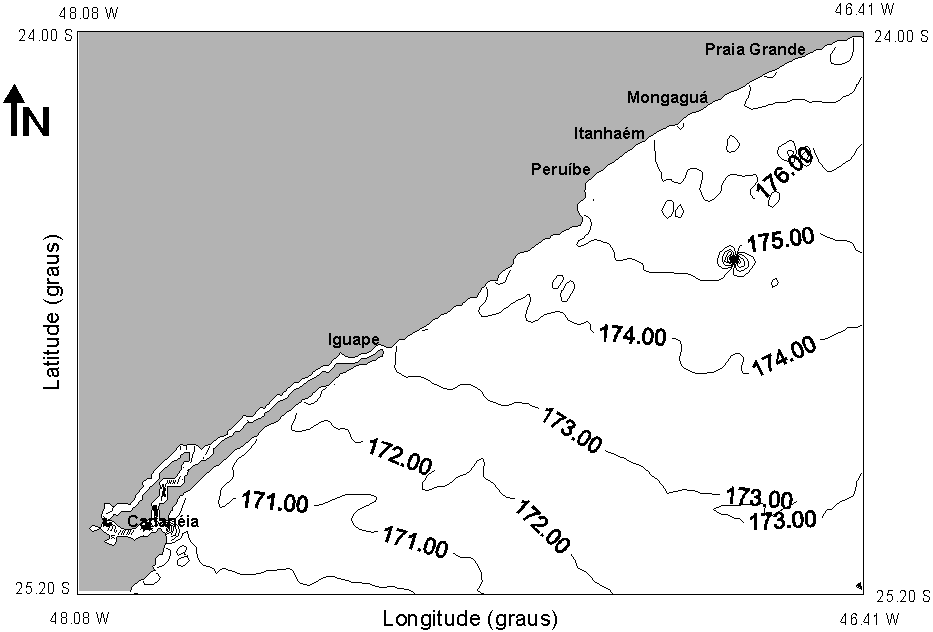
Fig. 4 – Cotidal maps of M2 component: amplitudes (cm) and phases relative to Greenwich (degrees), for the basic grid.
One interesting result generated by models of tidal propagation is the residual circulation, generally computed simply as the sum of hourly results of elevations and currents, considering a large number of complete tidal periods. In present study, the residual elevations and surface currents are presented on Figure 5, showing a resultant transport to Northeast, parallel to the coast.
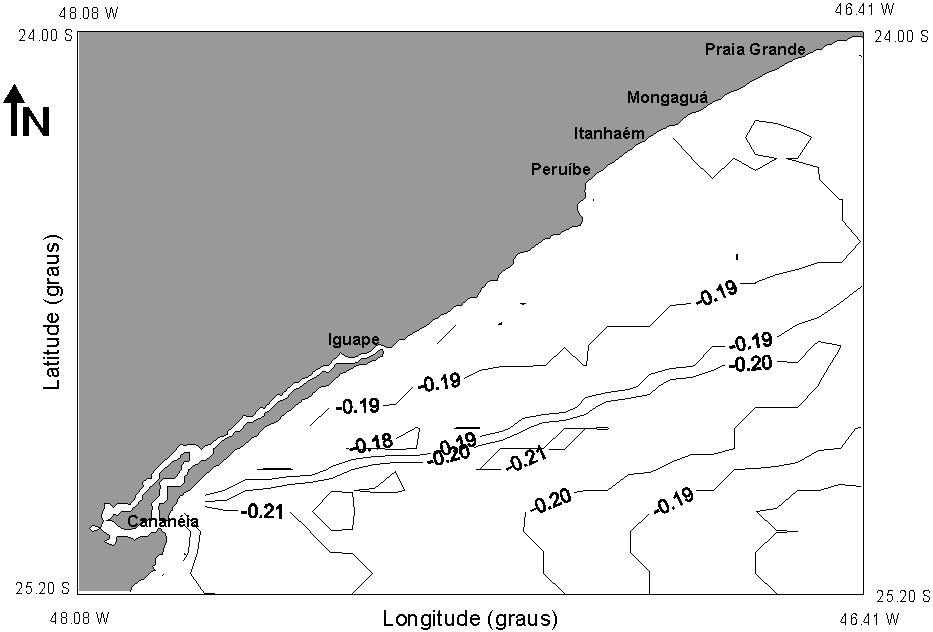
![]()
Fig. 5a- Residual elevations of the tidal circulation (cm).
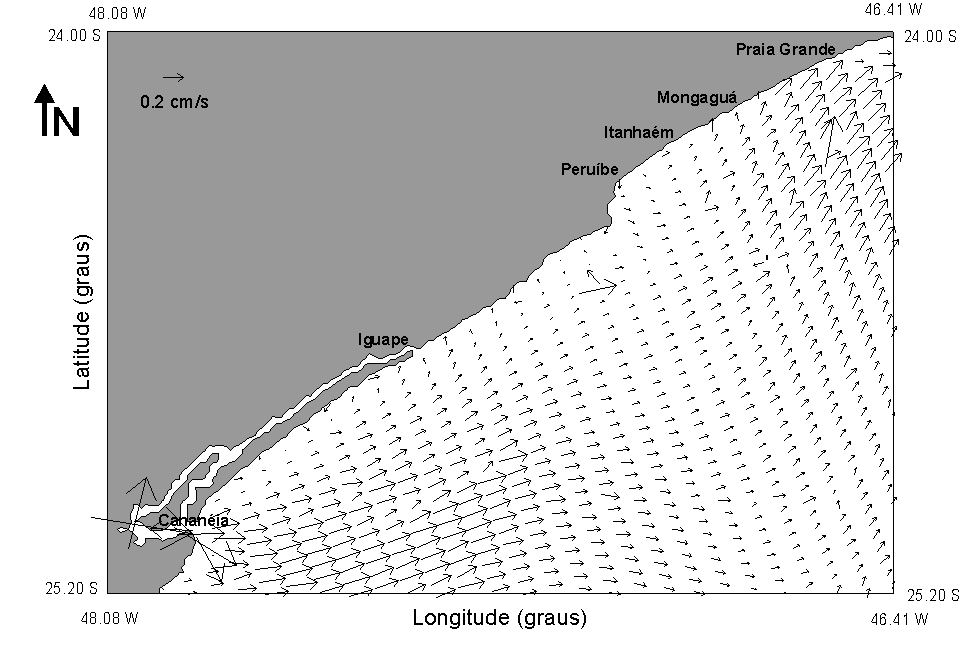
![]()
Fig. 5b- Surface residual currents of the tidal circulation.
The characteristics of the tidal circulation in the estuary agree with other researches in the area, such as the ones of Mesquita & Harari (1983) and Miyao & Harari (1989). Details of the model and the complete results of the tidal simulations can be found on Picarelli (2001). Actually, the model is running considering other forcings besides the tides – winds and density effects.
The implementation of the numerical model of the estuary of Cananeia – Iguape is very useful, since it provides an important tool for many practical and theoretical applications, such as: reproduction of the tidal components amplification in the area (especially M3), support to navigation and fishing, coastal protection, pollution control, among others.
References
Blumberg, A. F. & Mellor, G. L. 1987. A description of a three-dimensional coastal ocean circulation model. In: Heaps, N. S. ed. Three-Dimensional Coastal Ocean Models. Coastal and Estuarine Sciences, 4: 1-16.
Franco, A. S. 1988. Tides: fundamentals, analysis and prediction. Publicações do Inst. de Pesquisas Tecnológicas, S. Paulo, 232p.
Franco, A. S. & Harari, J. 1987. Computer programs for tidal data checking, correction, analysis and prediction by the harmonic method. Relat. Int. Inst. oceanogr., Univ. S. Paulo, 16: 1-65.
Harari, J. & Camargo, R. 1994 Simulação da propagação das nove principais componentes de maré na plataforma sudeste brasileira através de modelo numérico hidrodinâmico. Bolm. Inst. oceanogr., S. Paulo, 42(1): 35-54.
Mesquita, A. R. & Harari, J. 1983 Tides and tide gauges of Cananéia and Ubatuba, Brazil (lat 24º). Relat. Int. Inst. oceanogr., Univ. S. Paulo, 11: 1-14.
Miyao, S. Y. & J. Harari. 1989. Estudo preliminar da maré e das correntes de maré na região estuarina de Cananéia (25°S - 48°W). Bolm Inst. oceanogr., S. Paulo, 37(2): 107-123.
Picarelli, S. S. 2001 Modelagem numérica da circulação de maré na região costeira centro sul do Estado de São Paulo. Dissertação de Mestrado, IOUSP, 116p.