Abstract

The correlation coefficient, , is shown to depend on the ratio of two variances and then invariant on the inclination  of the regression line relative to the co-ordinated axes. Also invariant with the inclination  is the mean distance l of the discrete data points to the regression straight line.. Analysis of these coefficients (  and l ) and their invariance with rotation of the Cartesian co-ordinate system, from synthetic series, allowed the definition of a variable F =  x l, that is also invariant and may be taken as a constant which characterises each of the constrained planetary series and, in consequence, the F distribution of the entire set of PSMSL sea level series.

Trends, Regression and Distances

This communication explores relationships between parameters of time series data, such as trends,  angles  ,  = tan( ) , distances l of data points to the regression line, Fig 1, and correlations , with the aim of better understanding the geophysical information in a set of PSMSL ( Permanent Service for the Mean Sea Level) of IAPSO, ( International Association for the Physical Sciences of the Oceans)) sea level series (Spencer & Woodworth, 1993), evenly distributed around the oceans, taken here as a planetary data set. These series take values of trend , that appear to be physically constrained by the planet Earth, relative to its surface, to maximum values, say ,within  1.1 radians, as the planet, in the scale of years, does not change its volume, or shape abruptly.

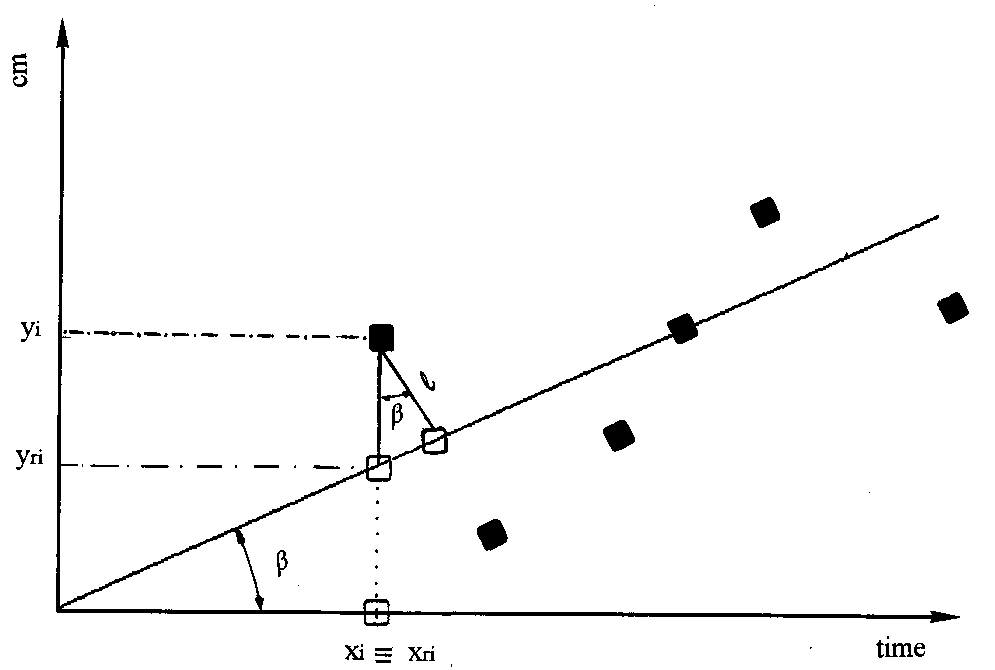
Fig. 1 - The regression line and its generating points (black spots). l is the distance of the point X(x_i, y_i), i=1,...,n, to the straight line. Its projection on the straight line X(x_ri, y_ri) is represented by a white square  is the inclination of the straight line relative to the x axis.

Free from these constraints 5,500 noisy ordinary time series, with 5 to 60 equivalent years lengths, were built, forced to acquire  values within about  40, and from them, the distances l, (the proximity of the data points to the straight line) and also the correlation coefficients , (the collinearity of the data points along the straight line) were calculated . Similarly, the distance l, in mm, the correlation coefficients , and, the corresponding trends , in mm/year, from real mean annual values of 837 planetary series, with different lengths, greater than 5 years, were calculated .

Collinearity and Proximity

The expressions usually utilised to express the data points were the distance l = (y(t_i) - y_ri(t_i))cos(), Fig 1, in terms of  and the Cartesian axes, the expressions of  in terms of the covariance (COV) of the points on the regression line ( y_ri(t_i) =  t_i +  ), and the actual data points y(t_i), divided by the variance (y_ri(t_i)) and also the collinearity coefficient , expressed in terms of the same covariance (COV), divided by the product of the standard deviations of (y_ri(t_i)) and (y(t_i)), i = 1,2,3,.......,n. (n = number of points of each series). The ratio of these standard deviations is shown to be a constant independent of the trends  as also are the distances l of the geometrical points to the regression line, i.e. their proximity to the line.

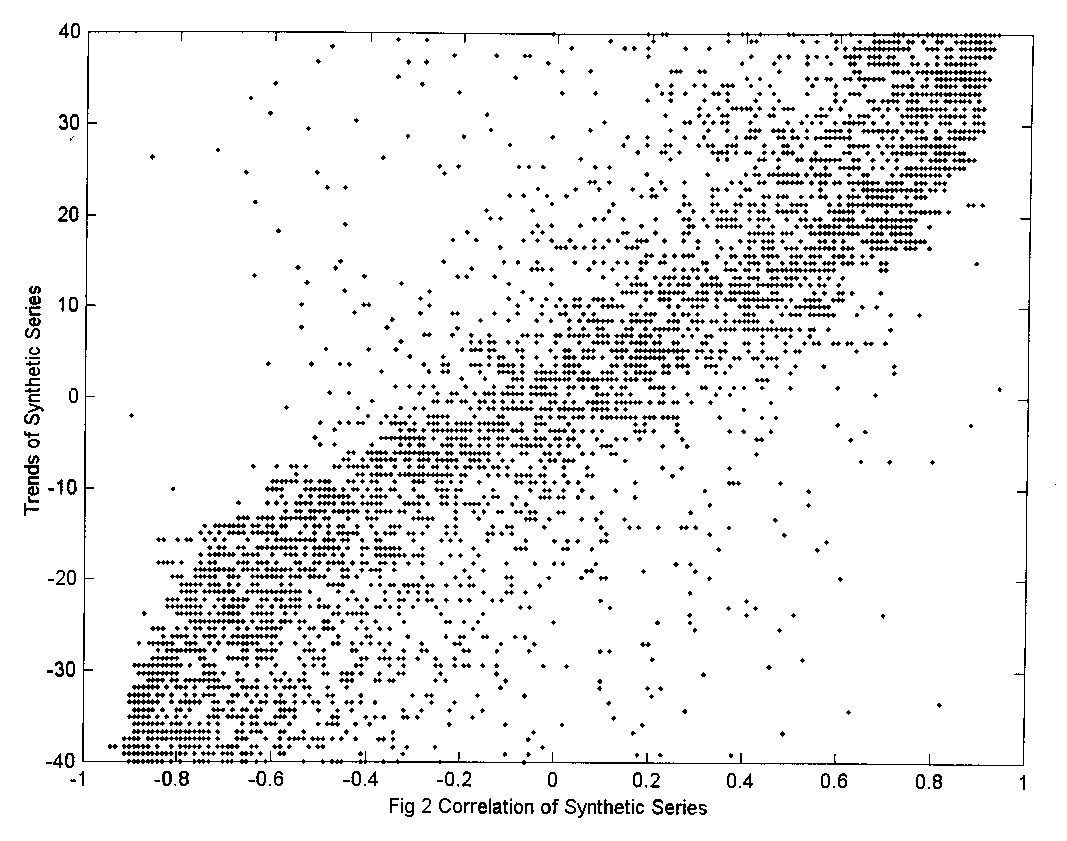
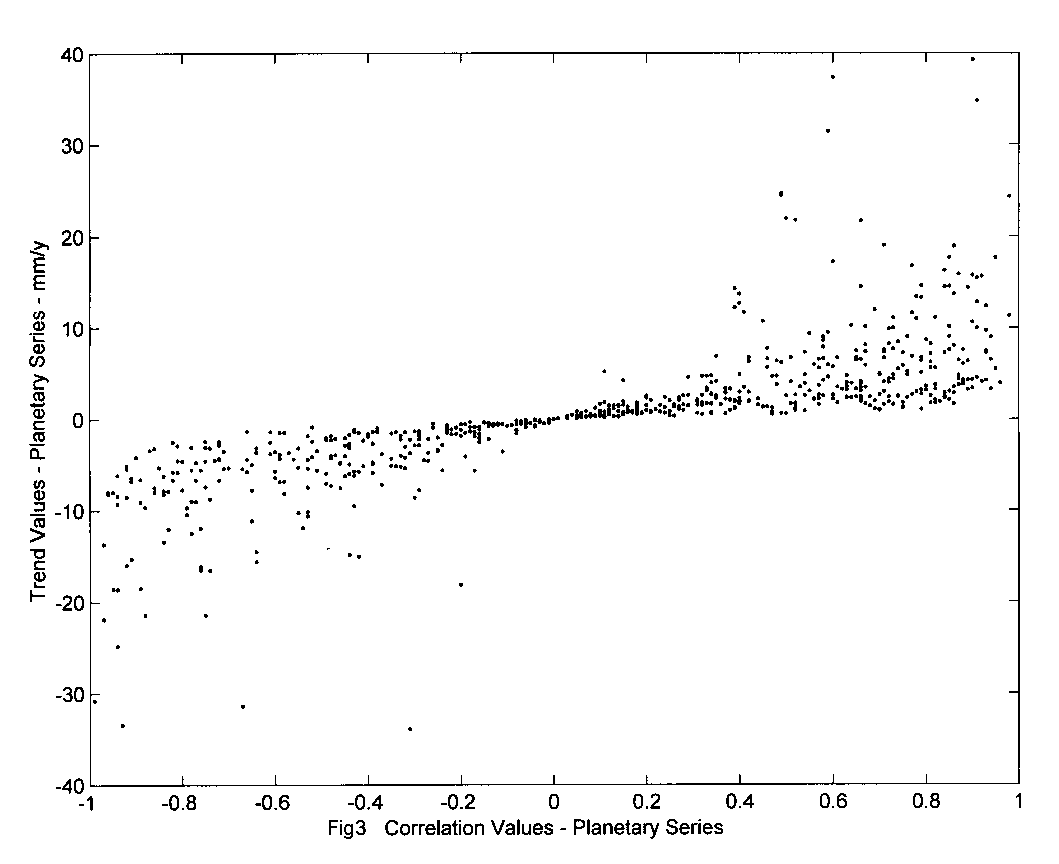
Results show that, while for the synthetic series collinearity  is independent of the values of the  as shown in Fig 2, the whole set of real series have values  that seem to be dependent of the trend . The plot of x  for PSMSL series, Fig 3, revealed a linear dependence, that should have not followed either or , as in fact they seem to be doing. This is interpreted as the unveiling of an Earth's action, that is imposed on the set of PSMSL planetary sea level series that is not seen from an individual series and requires the whole set of series to be detected and measured.
 
 

The F Distribution
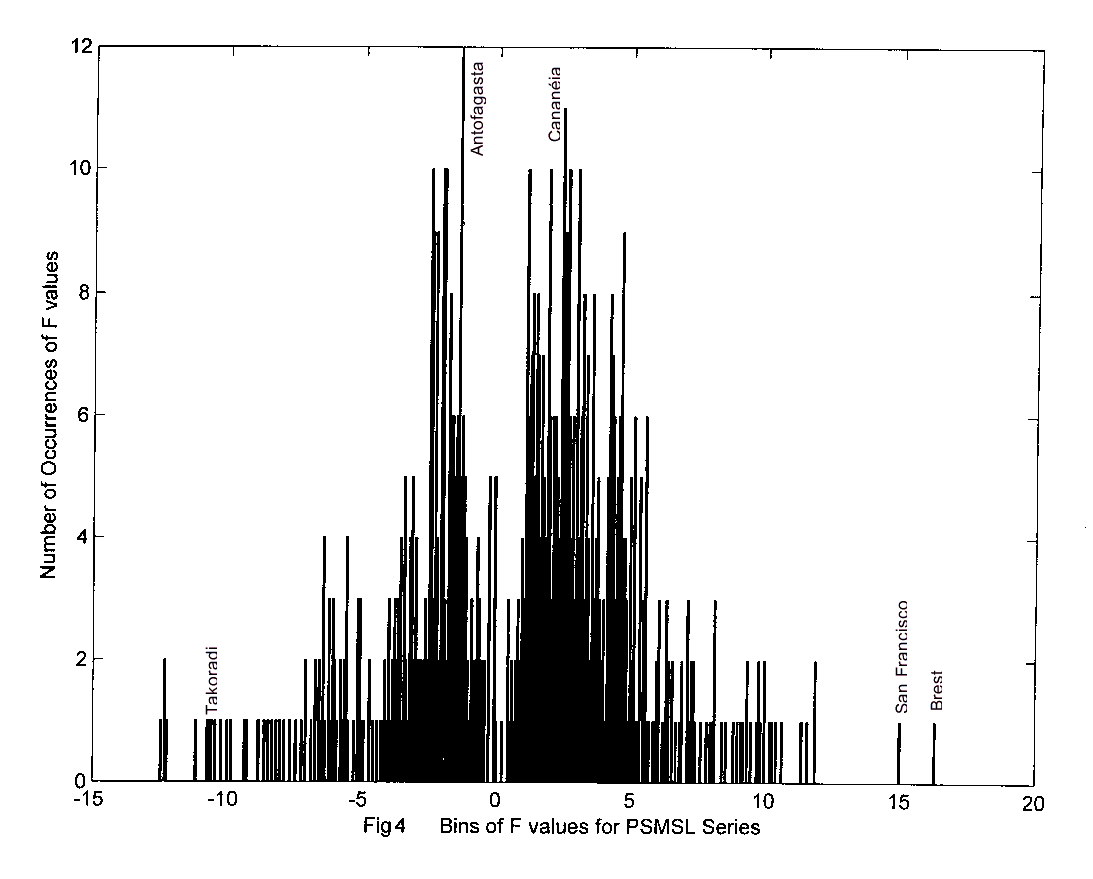
As l, the distances (mm) and  and  the correlation for a given planetary series, are both independent of the trend  (mm/year), a function F = l x  (mm) is defined, that is independent of the equivalent , which is, apparentely , also another characteristic of mass and gravity planetary series. The distribution curve of F may have, with the glaciations, an evolving timely constant shape, that is a characteristic of the Planet Earth, where in Fig 4, few identified ports of Africa, Europe and the Americas, should hold in the present days, relatively permanent positions as Takoradi, F = -11.14 mm; San Francisco, F = 14.95 mm; Balboa, F = 8.77 mm; Antofagasta, F = - 3.35 mm ; Cananeia, F = 4.56 mm and others.

Concluding Remarks

The correlation coefficient , taken as a measure of collinearity, and the mean distance l, taken as a measure of proximity of the discrete data points to the regression straight line, in time series, are both invariant on the inclination  of the regression line relative to the co-ordinated axes and in consequence their product.

The invariance of F = x l  values (mm) means that they are not dependent of trends  (mm/year) for each series. This causes the distribution of F values also to be independent of , which may be useful to examine aspects of the planet Earth that only arise from the study of world wide, evenly distributed planetary time series, as the set of PSMSL data.

Acknowledgements

We are grateful to Dr Philip Woodworth , Dr Ian Vassie and Robert and Elaine Spencer of POL (Proudman Oceanographic Laboratory), Liverpool, UK.

References

Jenkins, G M & Watts, D G , 1968 . Spectral Analysis and its Applications. Holden Day, London..523 p..

Spencer E N & Woodworth P L. 1993. Data Holdings of the Permanent Service for the Mean Sea Level. Bidston . Birkenhead. Merseyside, L437RA, UK. 81p.